深入探讨了Runge-Kutta方法在求解激光系统速率方程中的应用,特别是该方法在处理非线性方程组和复杂动力学行为时的优势。
项目信息
编号:MOG-41
大小:1.9M
运行条件
Matlab开发环境版本:
– Matlab R2020b、2023b
项目介绍
本文深入探讨了Runge-Kutta方法在求解激光系统速率方程中的应用,特别是该方法在处理非线性方程组和复杂动力学行为时的优势。激光系统的速率方程描述了腔内光子数密度与反转粒子数密度的动态变化,这些变化受一系列关键物理参数的影响,如增益介质的受激发射截面、腔长、激光器中的损耗、抽运速率和增益介质的上能级寿命等。通过这些物理参数的精确建模,能够准确模拟激光器在不同工况下的运行状态。
在本文的研究中,采用了四阶Runge-Kutta方法求解该速率方程。Runge-Kutta方法是一种数值积分技术,因其在处理非线性方程组时具有较高的稳定性和准确性而被广泛应用。相比于其他数值方法,如欧拉法或改进的欧拉法,四阶Runge-Kutta方法能够在不显著增加计算成本的情况下提供更高的精度,因此特别适用于激光系统这样对时间精度要求较高的场景。
通过MATLAB仿真,我们详细计算了光子密度和反转粒子数密度随时间的变化,绘制了光子数密度与反转粒子数密度的时间演化曲线,并将其与理论阈值进行对比。仿真结果清晰地揭示了激光器的动态特性,如光子密度的快速上升、系统的稳定运行阶段以及反转粒子数密度的逐渐下降。特别是,反转粒子数密度的临界阈值决定了激光器能否实现激光输出的关键,在仿真中得到了准确的展示。我们还进一步计算了激光器上能级状态的效率,验证了抽运速率与反转粒子数密度之间的关系,为激光器设计和优化提供了理论依据。
本研究展示了Runge-Kutta方法在解决复杂激光系统速率方程中的强大应用潜力。通过高精度的数值求解,该方法不仅能够揭示激光器内部的动态行为,还可以帮助工程师预测激光器在不同工作条件下的表现。未来,我们将进一步优化仿真模型,研究更多激光器系统中的非线性效应,如噪声影响、温度变化对激光性能的影响等,从而提升该方法在激光器设计中的应用价值。
项目文档
Tipps:可以根据您的需求进行写作,确保文档原创!
– 项目文档:写作流程

算法流程
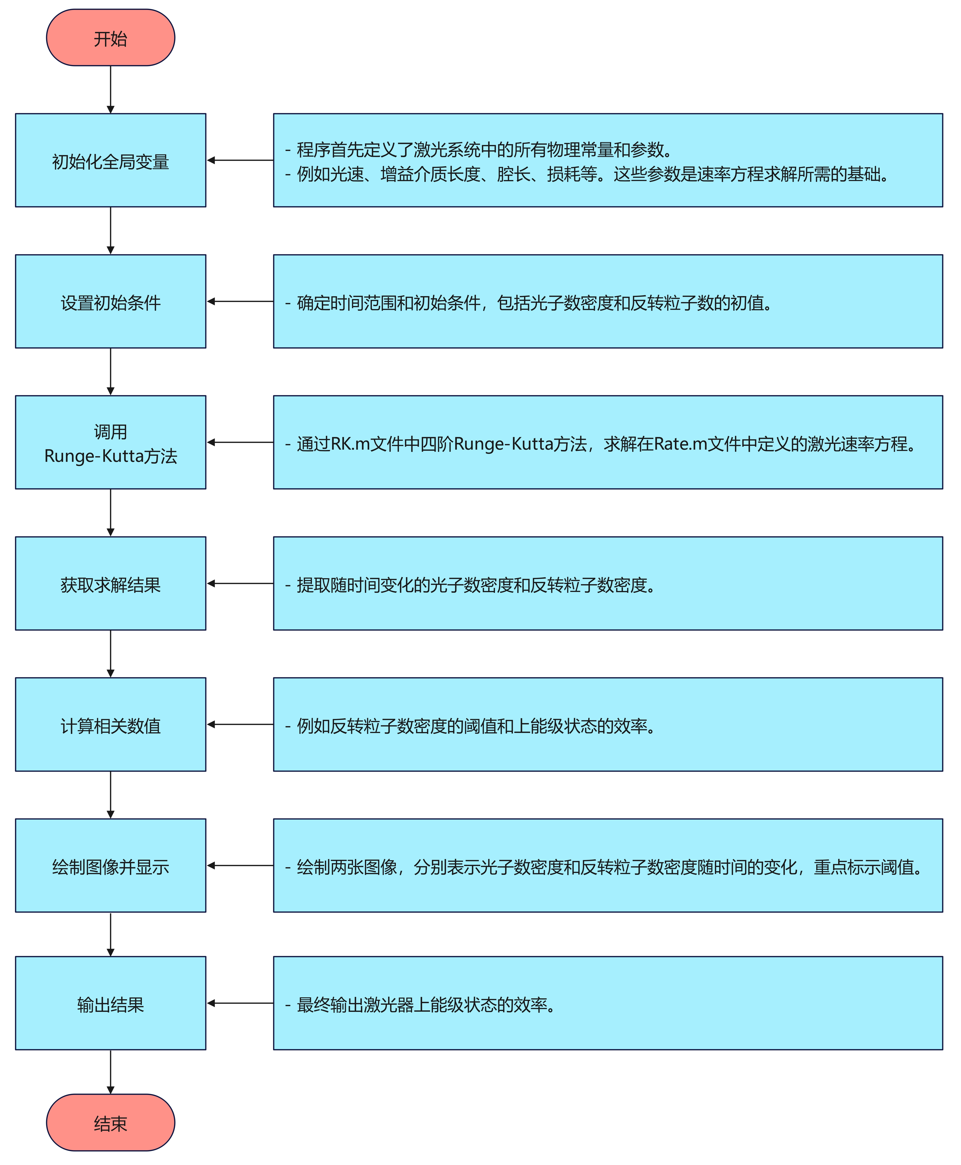
代码讲解
Tipps:仅对guipic.m部分代码简要讲解。该项目可以按需有偿讲解,提供后续答疑。

运行效果
运行 main.m
有两个子图:分别展示了光子数密度和反转粒子数密度随时间的变化关系。
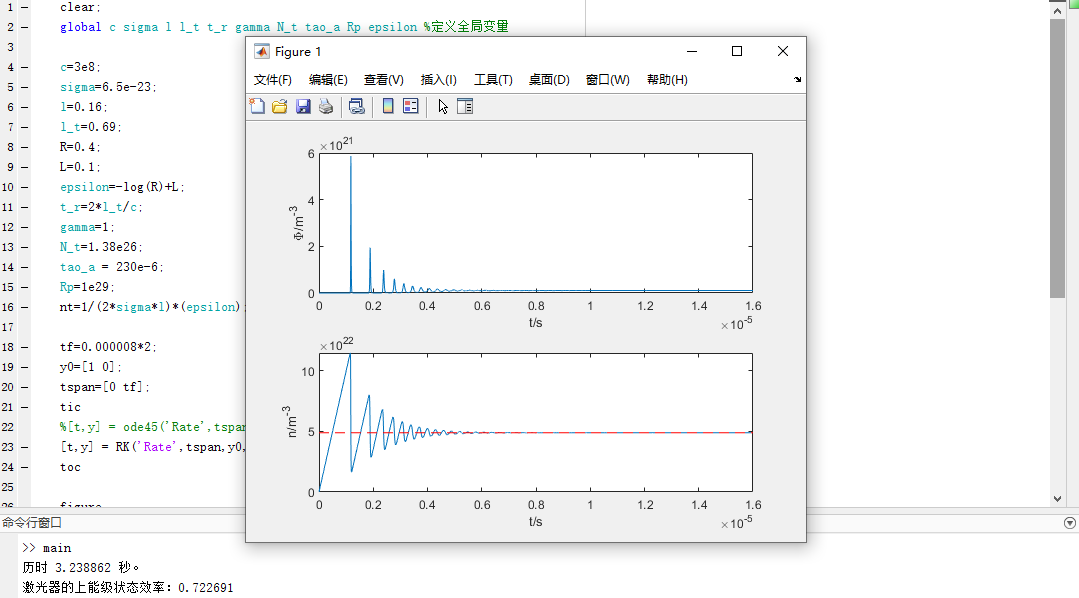
第一幅子图展示了激光腔内光子数密度随时间的动态变化,开始时迅速增加,然后逐渐减小并趋于平衡。
第二幅子图展示了反转粒子数密度的变化,初期大幅上升,随后逐渐接近阈值并趋于稳定。
整个图表反映了激光器从启动到达稳定状态的动态过程,包括光子数和反转粒子数的变化规律。
远程部署
Tipps:购买后可免费协助安装,确保运行成功。
– 远程工具:Todesk 、向日葵远程控制软件
– 操作系统:Windows OS
项目文件
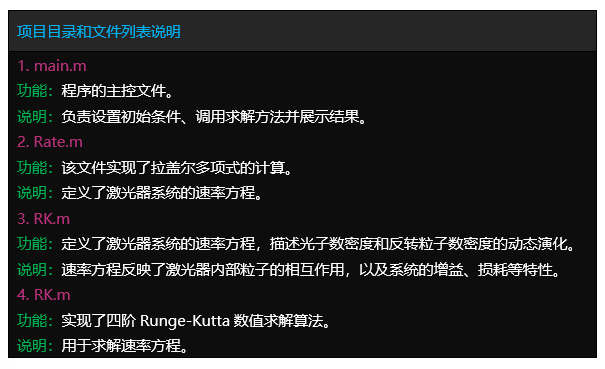
文件目录
Tipps:完整项目文件清单如下:
项目目录
– 1.Code (完整代码:确保运行成功)
– 2.Result (运行结果:真实运行截图)
– 3.Demo (演示视频:真实运行录制)



评论(0)