本研究提出了一种基于小波阈值滤波的信号去噪方法,旨在通过小波变换和灵活的阈值选择策略,有效地去除信号中的噪声成分。小波变换作为一种时频分析工具,可以将信号在不同尺度上进行分解,从而将信号的细节与噪声分离开来。本文在实验中首先生成了理想的仿真信号,并在该信号上叠加白噪声,模拟真实环境中的信号污染情况,以验证去噪方法的实际效果。接着,采用了一系列自定义的阈值函数来适配不同的噪声环境,并选择合适的小波分解层数,以实现信号的多层次分解与重构,最终有效抑制噪声的干扰。
项目信息
编号:MCV-63
大小:43M
运行条件
Matlab开发环境版本:
– Matlab R2020b、R2023b、R2024a
项目介绍
本文提出了一种基于小波阈值滤波的信号去噪方法,旨在通过小波变换和灵活的阈值选择策略,有效地去除信号中的噪声成分。小波变换作为一种时频分析工具,可以将信号在不同尺度上进行分解,从而将信号的细节与噪声分离开来。本文在实验中首先生成了理想的仿真信号,并在该信号上叠加白噪声,模拟真实环境中的信号污染情况,以验证去噪方法的实际效果。接着,采用了一系列自定义的阈值函数来适配不同的噪声环境,并选择合适的小波分解层数,以实现信号的多层次分解与重构,最终有效抑制噪声的干扰。
实验结果表明,基于小波阈值滤波的去噪方法不仅能够显著降低噪声,还能在去噪后较好地保持信号的主要特征和结构,避免了信号过度平滑或细节损失等问题。为量化去噪效果,本文采用了多项评价指标,包括信噪比 (SNR)、均方误差 (MSE) 和波形相似系数 (NCC)。实验数据显示,该方法在不同阈值选择策略下均表现出较高的去噪效果,其中SNR值较高,MSE值较低,NCC值接近1,表明滤波后的信号与原始信号具有高度相似性,从而验证了该方法的有效性和适用性。
本文所研究的基于小波阈值的信号去噪方法为信号处理领域提供了一种高效且具有调节灵活性的去噪方案。该方法不仅可以应用于一维信号的去噪,也可推广到其他类型信号的噪声抑制处理,为信号分析、图像处理及生物医学等领域的噪声去除提供了新的思路和理论支持。
项目文档
Tipps:可以根据您的需求进行写作,确保文档原创!
– 项目文档:写作流程

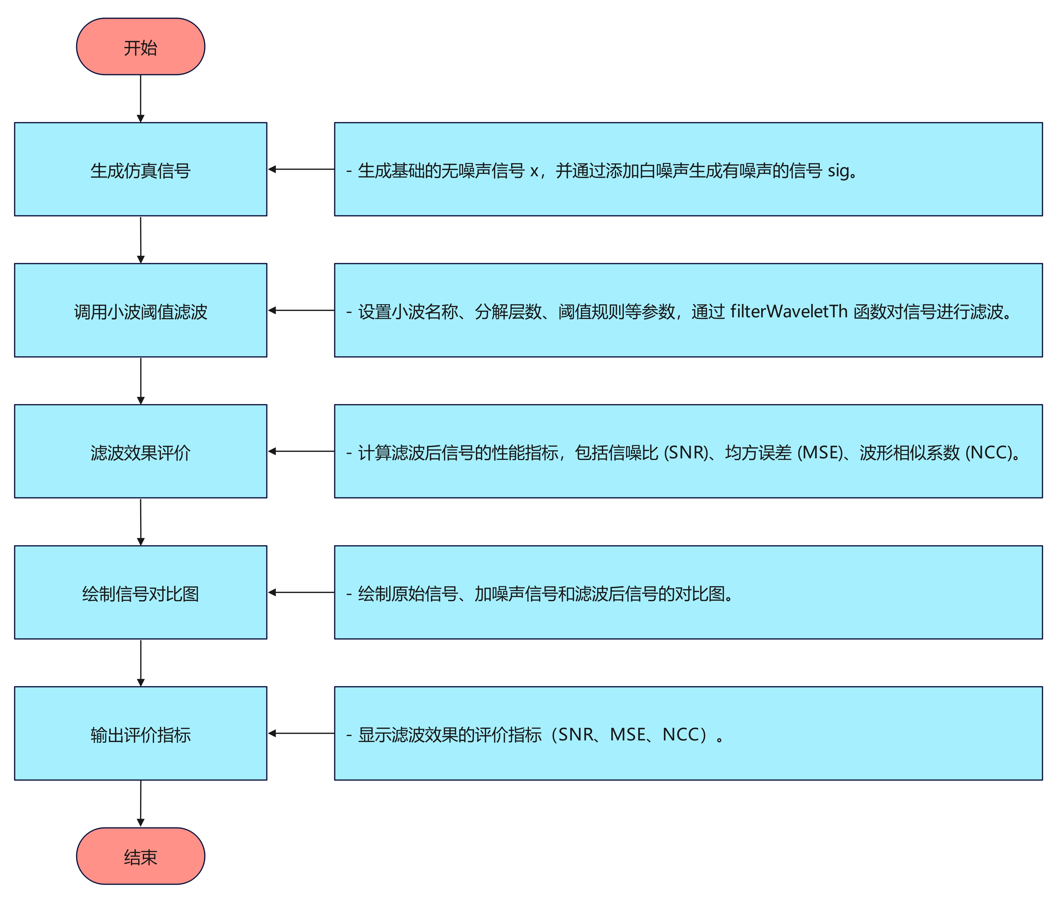
算法流程
代码讲解
Tipps:仅对demoWaletThFilter.m部分代码简要讲解。该项目可以按需有偿讲解,提供后续答疑。

运行效果
运行 demoWaletThFilter.m
图1显示的信号的预测值和真实值在不同时间点的对比图:
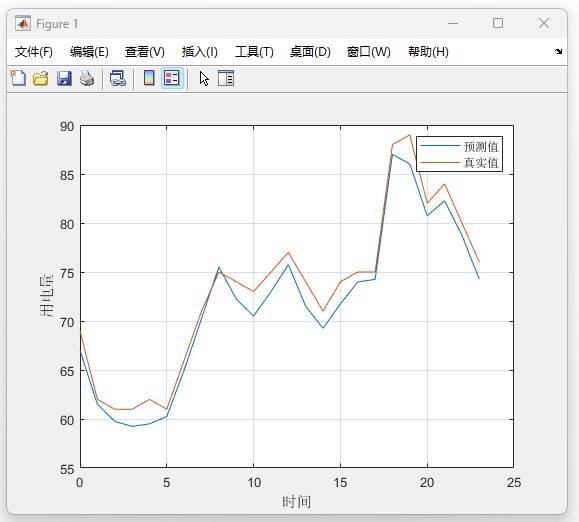
横轴表示时间,纵轴表示信号值。图中的两条曲线(预测值和真实值)显示了信号在时间上的变化趋势。这种对比通常用于验证预测模型的准确性,曲线越接近说明模型的预测效果越好。
图2展示了两个子图:
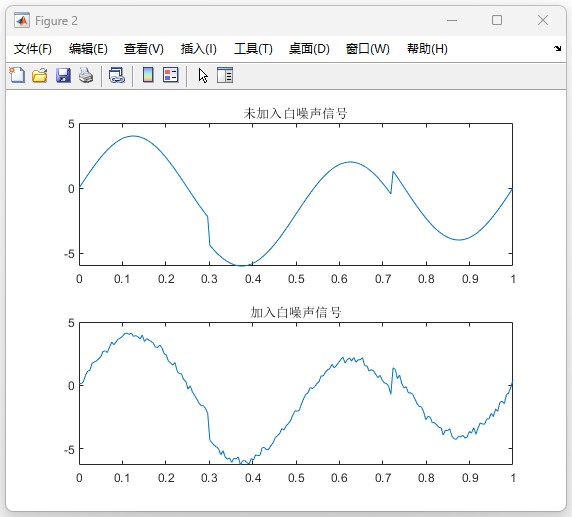
(1)上图:未加入噪声的信号。
(2)下图:加入了白噪声的信号。
这些图显示了噪声对信号的影响。上图中的信号较为平滑,而下图的信号则因噪声的加入而出现波动,这种对比用于显示噪声对信号的影响。
图3包含三个子图:
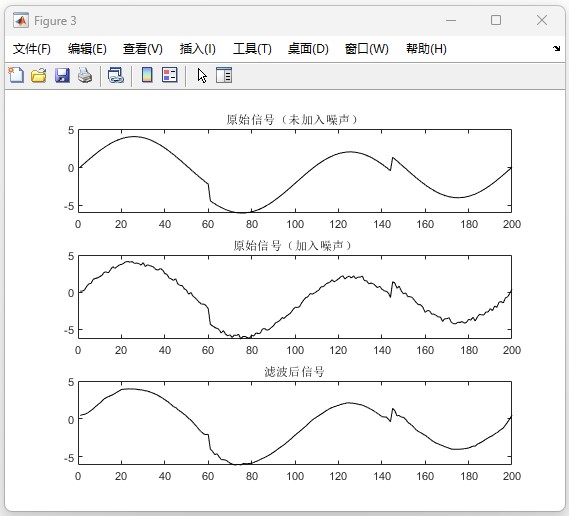
(1)第一行:原始信号(未加入噪声)。
(2)第二行:加入噪声后的信号。
(3)第三行:经过小波阈值滤波后的信号。
这三个图展示了信号在不同处理阶段的变化,能够直观地看到滤波前后的效果对比。经过滤波后,信号恢复了原始信号的平滑特征,说明滤波器有效地去除了噪声。
图4终端输出
![]()
滤波后的SNR、MSE和NCC值分别为:29.0521、0.011805、0.99938
(1)SNR(信噪比):较高的值(如29.0521)表明滤波后的信号质量较好。
(2)MSE(均方误差):较低的值(如0.011805)表明滤波后信号与原始信号的差异较小。
(3)NCC(波形相似系数):接近1的值(如0.99938)表明滤波后的信号与原始信号的形状非常相似。
通过这些图与指标,您可以分析滤波效果,确认小波阈值滤波的去噪能力。
远程部署
Tipps:购买后可免费协助安装,确保运行成功。
– 远程工具:Todesk 、向日葵远程控制软件
– 操作系统:Windows OS
项目文件
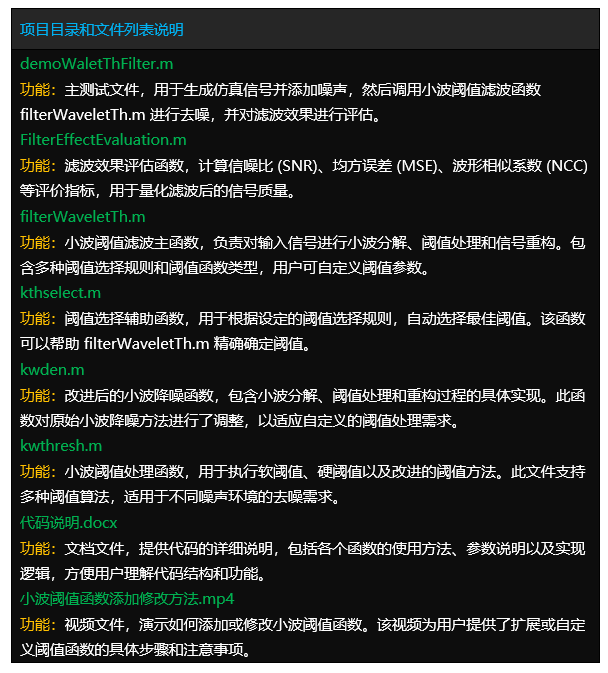
文件目录
Tipps:完整项目文件清单如下:
项目目录
– 1.Code (完整代码:确保运行成功)
– 2.Result (运行结果:真实运行截图)
– 3.Demo (演示视频:真实运行录制)



评论(0)