在复杂环境中的路径规划问题中,PRM(概率路网)和Dijkstra算法是两种常用的路径搜索方法。
项目信息
编号:POG-3
大小:24M
运行条件
Python开发环境:
– PyCharm的安装包:PyCharm: Python IDE for Professional Developers
– PyCharm的历史安装包:PyCharm: Python IDE for Professional Developers
– Anaconda的安装包:Anaconda | Start Coding Immediately
– Python开发版本:Python==3.9
需要安装依赖包:
– pip install numpy==1.24.0
– pip install GDAL==3.3.2
– pip install pillow==10.4.0
– pip install matplotlib==3.9.2
项目介绍
在复杂环境中的路径规划问题中,PRM(概率路网)和Dijkstra算法是两种常用的路径搜索方法。本文提出了一种将PRM算法与Dijkstra算法相结合的路径规划方法。该方法首先利用PRM算法在环境中随机生成节点,并通过碰撞检测构建节点之间的连通图。随后,使用Dijkstra算法在构建的图上搜索从起点到目标点的最优路径。实验表明,该方法在确保路径有效性的同时能够在复杂障碍环境中有效规划出最短路径。本文进一步讨论了障碍物的处理和路径优化过程,并通过可视化展示了路径规划的效果。
项目文档
Tipps:可以根据您的需求进行写作,确保文档原创!
– 项目文档:写作流程

算法流程
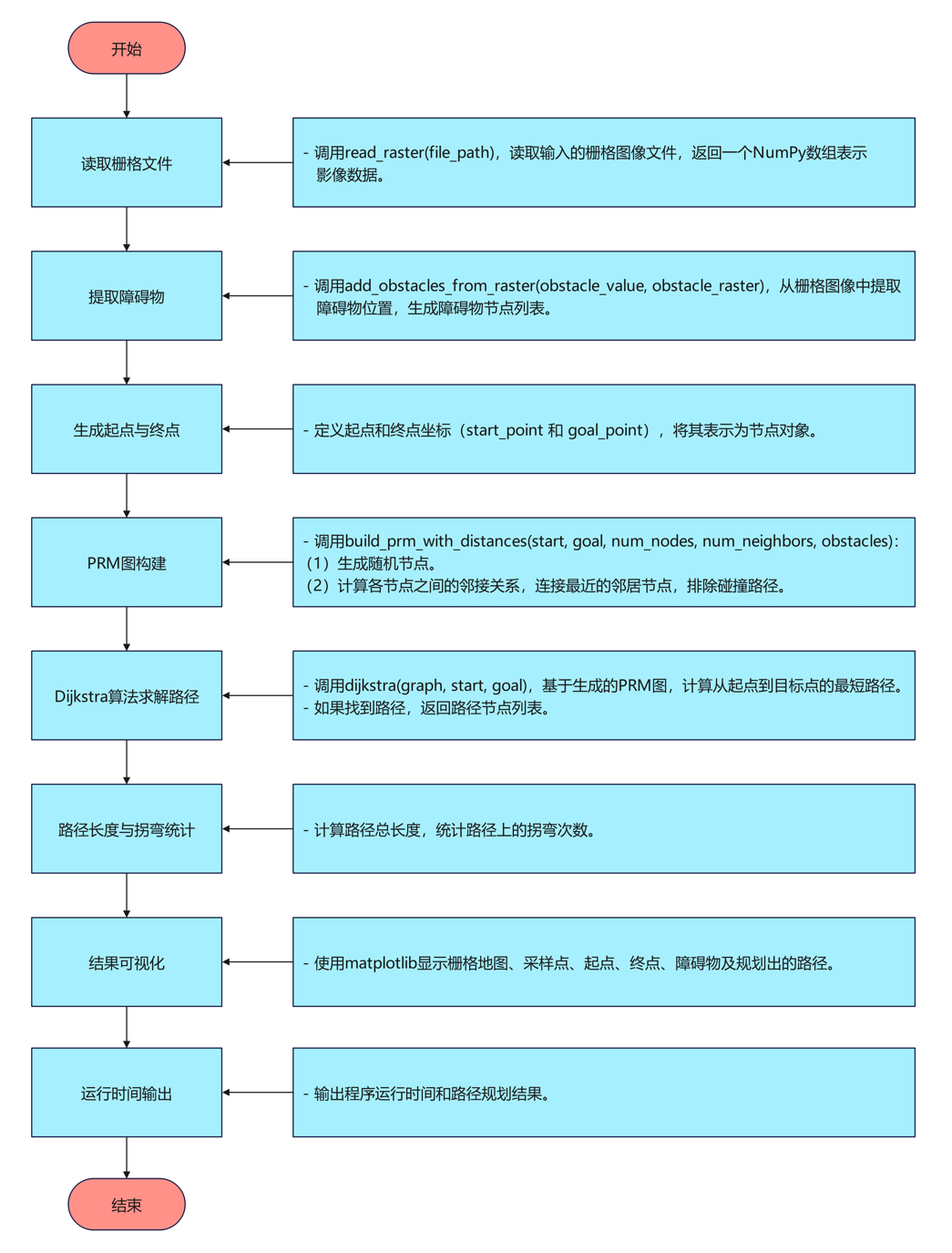
代码讲解
Tipps:仅对PRM算法和Dijkstra算法结合.py部分代码简要讲解。该项目可以按需有偿讲解,提供后续答疑。

运行效果
– 运行 PRM算法和Dijkstra算法结合.py
图形化路径规划结果
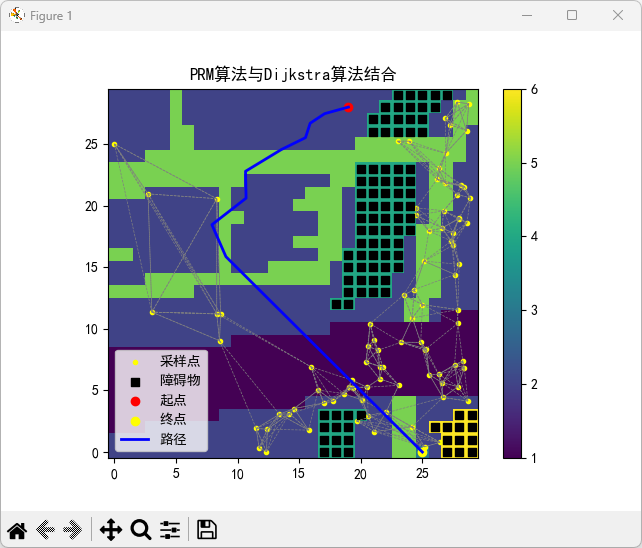
1.背景栅格图:这张图是一个彩色的栅格地图,显示了不同颜色代表的地形或障碍物区域。
(1)颜色条(右侧):表示栅格图中不同区域的值范围,颜色从深紫色到亮黄色逐渐变化,可能表示高度或其他地形信息。
2.黄色点:表示PRM算法生成的随机采样点。这些点是通过概率路网(PRM)算法随机生成的候选路径节点。
3.黑色方块:表示障碍物。程序从栅格数据中提取了障碍物的位置,并在路径规划时进行了碰撞检测,避免路径穿越障碍物。
4.红色圆点:表示路径规划的起点。
5.黄色圆点:表示路径规划的终点。
6.蓝色线条:表示使用Dijkstra算法找到的从起点到终点的最优路径。该路径是在已经生成的PRM采样点和构建的图上搜索出来的。
7.灰色虚线:表示PRM算法连接的各个采样点之间的边,这些边代表了可以行进的路径。
8.图例:图例标注了不同颜色和符号的含义,帮助解释图中的采样点、障碍物、起点、终点和路径。
控制台输出

1.最短路径的总代价:控制台输出显示了最短路径的总代价,但由于是Node对象,显示的是对象的内存地址,未显示具体代价值。
2.总运行时间:程序的运行时间为16.5612秒,这是从路径规划算法开始到完成所消耗的时间。
3.路径拐弯个数:路径上的拐弯次数为8次,这表明路径在到达终点的过程中发生了8次方向上的变化。
4.路径的总长度:总路径长度为41.2453栅格单位,这是从起点到终点的最短路径的距离。
综上,这两张图展示了PRM和Dijkstra算法结合后在复杂地形中寻找最短路径的效果,并通过图形化的方式清晰展示了采样点、障碍物和路径的分布情况。
远程部署
Tipps:购买后可有偿协助安装,确保运行成功。
– 远程工具:Todesk 、向日葵远程控制软件
– 操作系统:Windows OS
项目文件
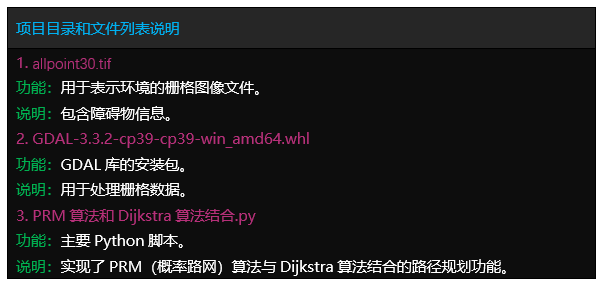
文件目录
Tipps:完整项目文件清单如下:
项目目录
– 1.Code (完整代码:确保运行成功)
– 2.Result (运行结果:真实运行截图)
– 3.Demo (演示视频:真实运行录制)



评论(0)