本文提出了一种基于改进蚁群算法的最短路径优化方法。
项目信息
编号:MOG-32
大小:4.3M
运行条件
Matlab开发环境版本:
– Matlab R2020b、R2023b
项目介绍
蚁群算法是一种模仿蚂蚁觅食行为的优化算法,具有全局寻优能力强、并行计算等优点。然而,传统蚁群算法在复杂环境中容易出现局部收敛、路径选择不稳定等问题。针对这些问题,本文对蚁群算法进行了改进,通过引入弯曲因子和路径长度的优化策略,使得算法在复杂地形环境下能够更快速、更稳定地收敛到全局最优路径。仿真实验结果表明,改进后的蚁群算法在路径规划中的性能优于传统算法,具有更好的收敛性和稳定性。
项目文档
Tipps:可以根据您的需求进行写作,确保文档原创!
– 项目文档:写作流程

算法流程
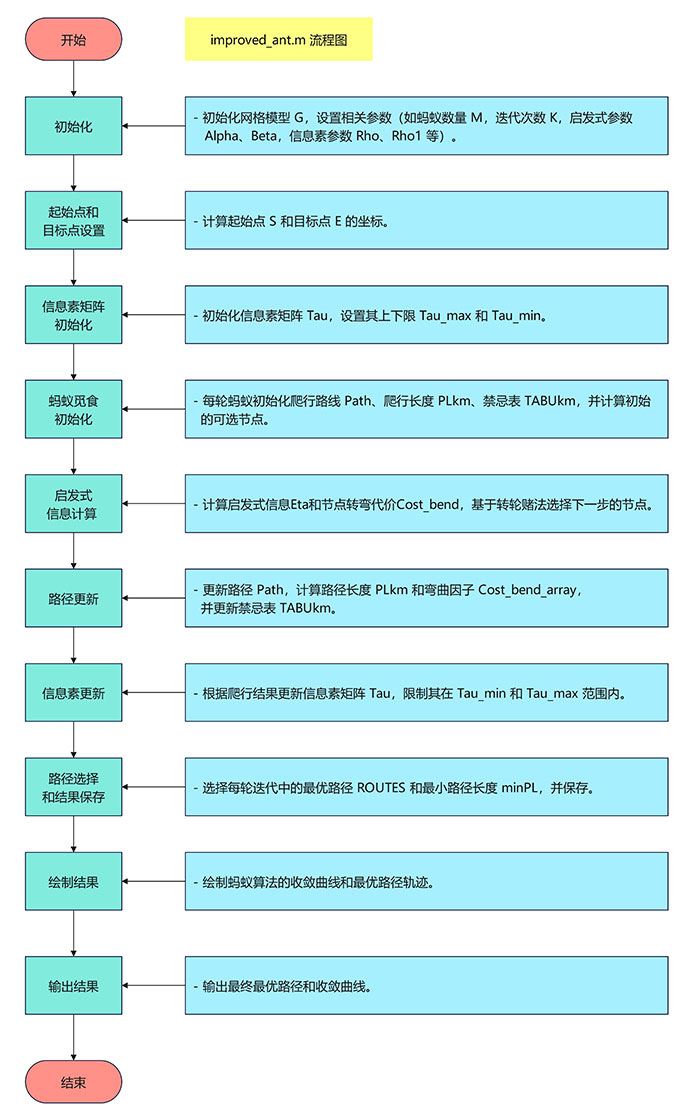
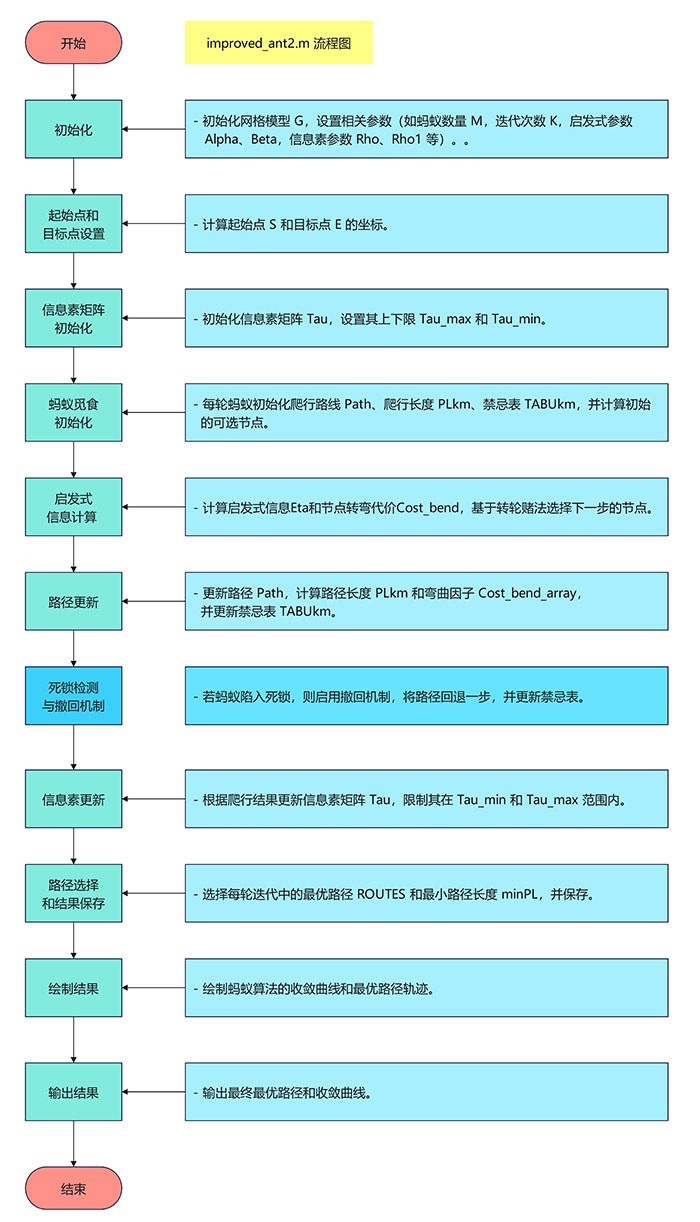
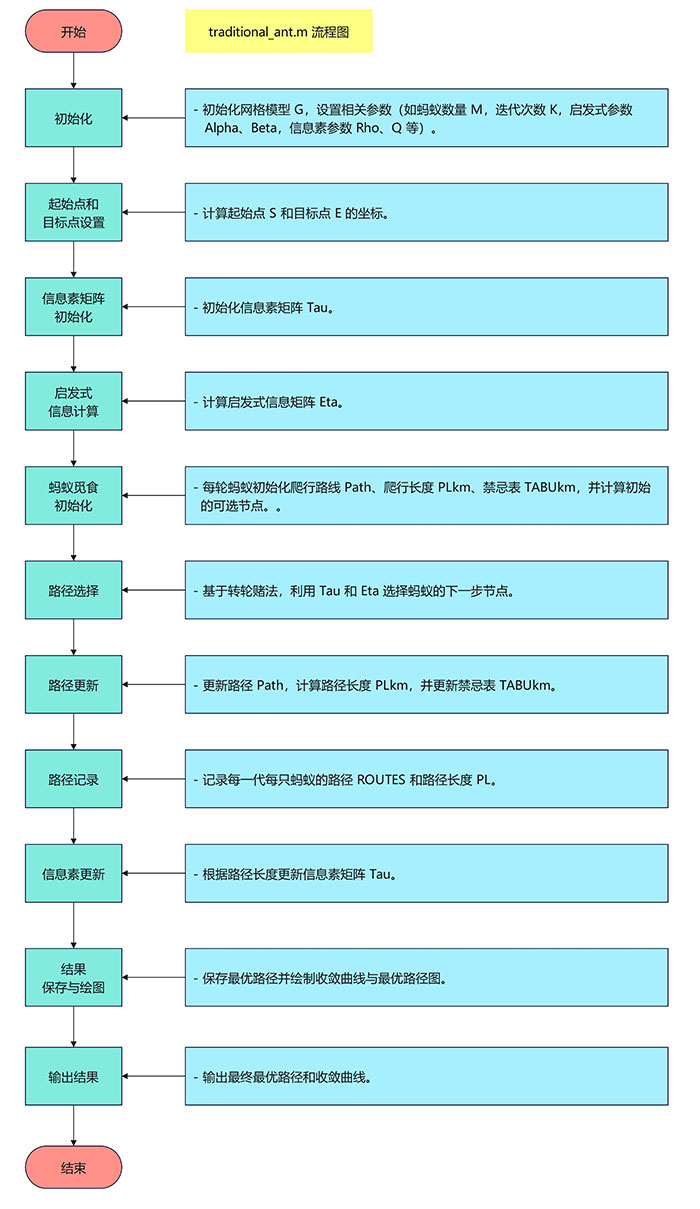
代码讲解
Tipps:仅对improved_ant.m部分代码简要讲解。该项目可以按需有偿讲解,提供后续答疑。

运行效果
运行 improved_ant.m
收敛曲线图
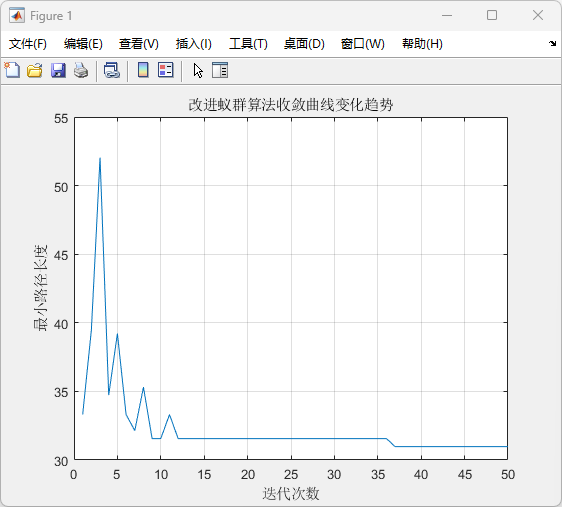
(1)该图展示了蚁群算法在不同迭代次数下的最小路径长度的变化趋势。
(2)横轴表示迭代次数(蚂蚁群体在寻找最优路径的次数)。
(3)纵轴表示最小路径长度。
(4)从图中可以看到,随着迭代次数的增加,最小路径长度逐渐减少,并趋于稳定。这表明随着蚂蚁群体的搜索过程,算法能够逐步找到更优的路径,最终收敛到一个较好的解。
路径轨迹图

(1)该图展示了改进蚁群算法在一个二维障碍物环境中的最优路径选择。
(2)横轴和纵轴分别表示坐标x和坐标y,黑色方块表示障碍物,白色区域表示可通行的路径。
(3)红色线条表示蚂蚁找到的从起点到终点的最优路径。
(4)从图中可以看到,算法成功地在复杂的障碍物环境中规划出一条避开障碍物的最优路径,这条路径是蚂蚁在多次迭代过程中逐渐收敛并最终选择的结果。
这两幅图展示了改进蚁群算法在路径规划中的有效性和收敛性,图1说明了算法的收敛过程,而图2则展示了算法找到的具体最优路径。
运行 improved_ant2.m
收敛曲线图
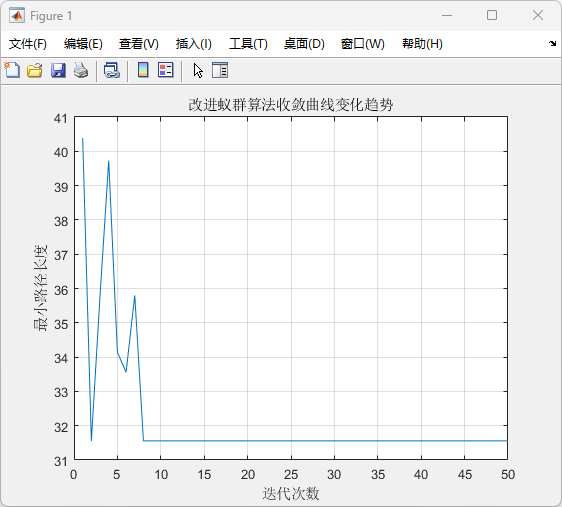
(1)该图展示了蚁群算法在不同迭代次数下的最小路径长度的变化趋势。
(2)横轴表示迭代次数(蚂蚁群体在寻找最优路径的次数)。
(3)纵轴表示最小路径长度。
(4)从图中可以看到,最小路径长度在前几次迭代中波动较大,随后趋于稳定。这表明随着算法的进行,路径逐渐优化,最终收敛到一个较短的路径长度。这种稳定性体现了改进后的蚁群算法在找到最优路径时的有效性。
路径轨迹图
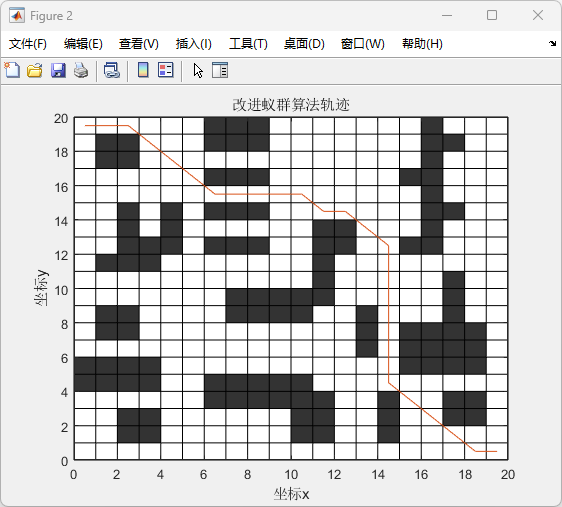
(1)该图展示了改进蚁群算法在一个二维障碍物环境中的最优路径选择。
(2)横轴和纵轴分别表示坐标x和坐标y,黑色方块表示障碍物,白色区域表示可通行的路径。
(3)红色线条表示蚂蚁找到的从起点到终点的最优路径。
(4)从图中可以看到,算法成功地在复杂的障碍物环境中规划出一条避开障碍物的最优路径,这条路径是蚂蚁在多次迭代过程中逐渐收敛并最终选择的结果。
这两幅图展示了改进蚁群算法在路径规划中的有效性和收敛性,图1说明了算法的收敛过程,而图2则展示了算法找到的具体最优路径。
运行 traditional_ant.m
收敛曲线图
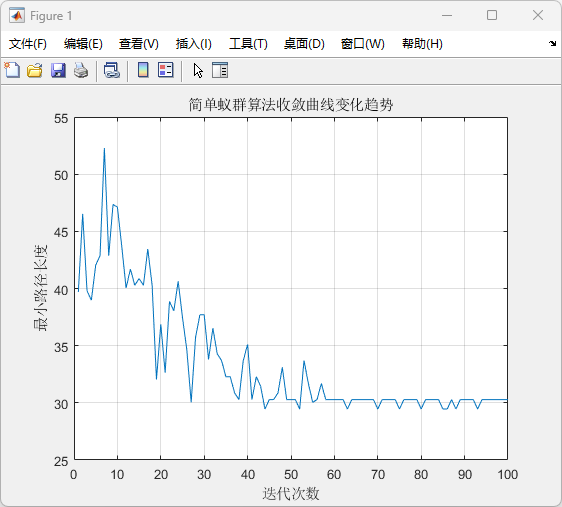
(1)该图展示了简单蚁群算法在不同迭代次数下的最小路径长度的变化趋势。
(2)横轴表示迭代次数,纵轴表示最小路径长度。
(3)从图中可以看到,最小路径长度在前几次迭代中波动较大,随着迭代次数的增加,路径长度逐渐减少并趋于稳定。这表明蚁群算法在多次迭代后,逐渐找到了较优的路径,并且随着算法的进行,收敛性逐渐增强。
路径轨迹图
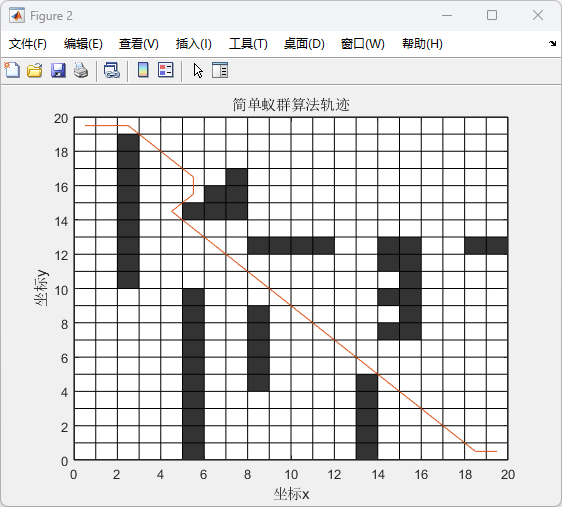
(1)该图展示了简单蚁群算法在二维障碍物环境中的最优路径选择。
(2)横轴和纵轴分别表示坐标x和坐标y,黑色方块表示障碍物,白色区域表示可通行的路径。
(3)红色线条表示蚂蚁找到的从起点到终点的最优路径。
(4)从图中可以看到,蚂蚁在避开障碍物的同时,成功地从起点到达终点,选择了一条较为直观且避障合理的路径。
这两幅图展示了简单蚁群算法的有效性。图1展示了算法在多次迭代中逐渐收敛到一个较短路径,而图2则展示了算法在二维空间中规划的最优路径。
远程部署
Tipps:购买后可免费协助安装,确保运行成功。
– 远程工具:Todesk 、向日葵远程控制软件
– 操作系统:Windows OS
项目文件
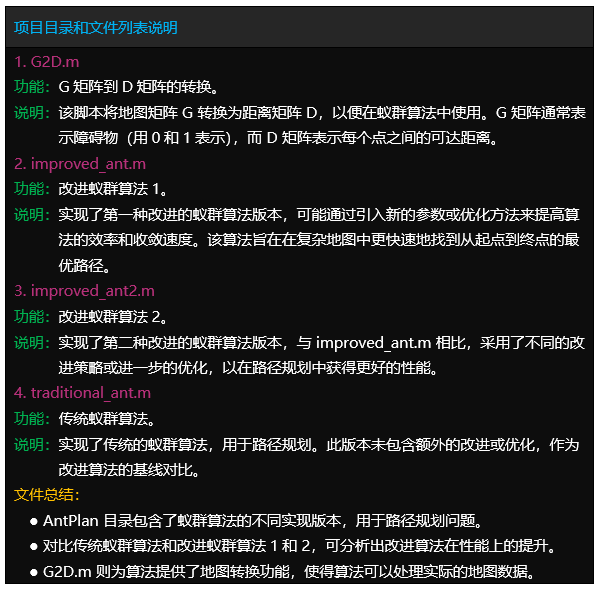
文件目录
Tipps:完整项目文件清单如下:
项目目录
– 1.Code (完整代码:确保运行成功)
– 2.Result (运行结果:真实运行截图)
– 3.Demo (演示视频:真实运行录制)



评论(0)