自适应滤波器在信号处理领域具有广泛的应用,尤其在噪声抑制、回声消除和信道均衡等场景中表现出色。
项目信息
编号:MOG-77
大小:2.5M
运行条件
Matlab开发环境版本:
– Matlab R2020b、2023b、2024a
项目介绍
自适应滤波器在信号处理领域具有广泛的应用,尤其在噪声抑制、回声消除和信道均衡等场景中表现出色。本文设计并实现了一种基于最小均方(LMS)算法的自适应滤波器,主要用于从带噪信号中提取期望信号。本文详细描述了LMS算法的原理、信号生成过程以及滤波器权重的更新机制,并分析了步长因子和滤波器阶数对滤波性能的影响。实验结果表明,经过LMS算法处理后,信号的信噪比显著提升,滤波器能够有效减小噪声干扰。此外,通过对比不同步长因子下的误差信号,验证了步长因子对滤波收敛速度和稳定性的显著影响。本研究为实际信号处理应用中的滤波器设计提供了理论参考和实验依据。
项目文档
Tipps:可以根据您的需求进行写作,确保文档原创!
– 项目文档:写作流程

算法流程
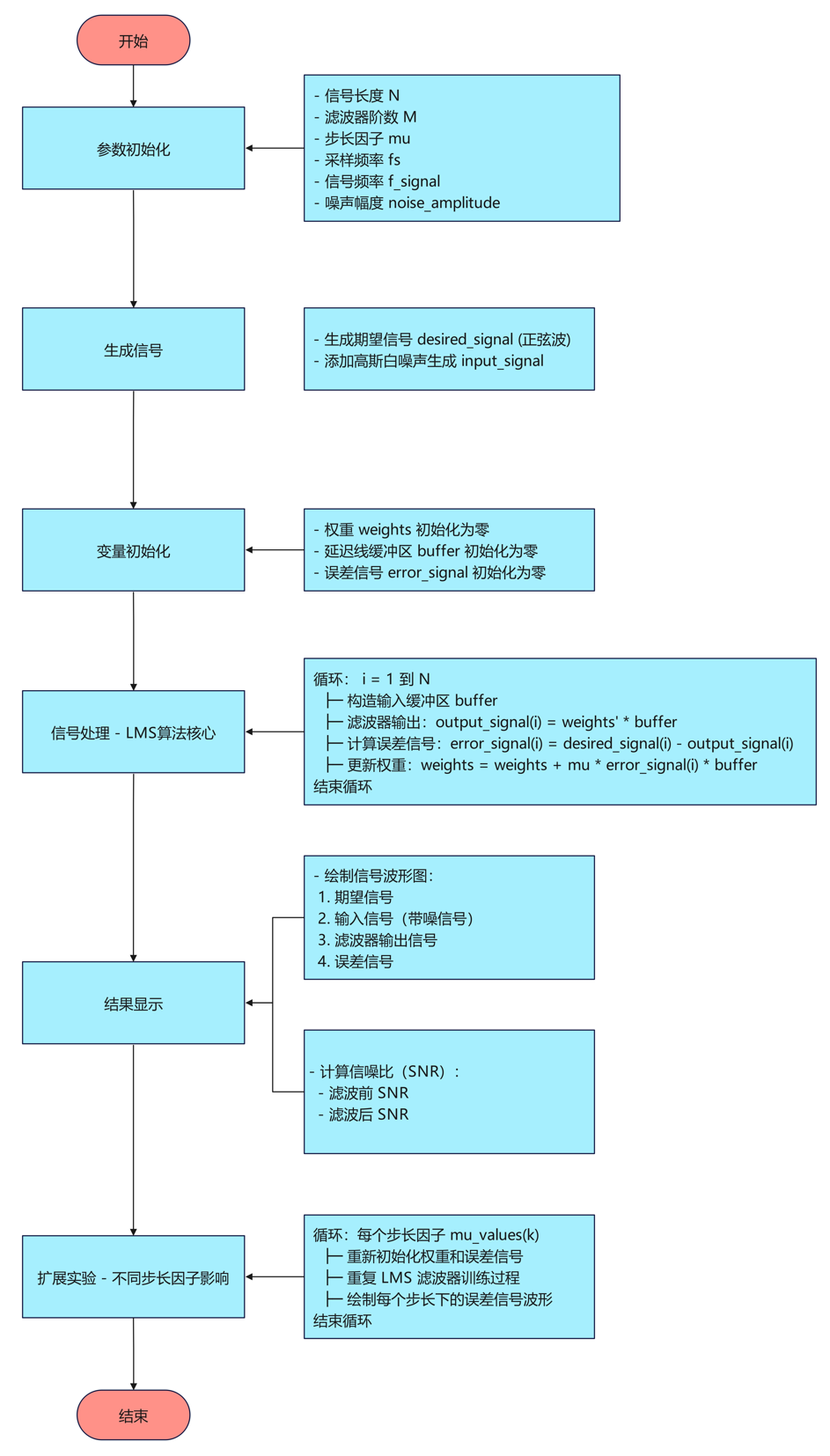
代码讲解
Tipps:仅对运行main.m部分代码简要讲解。该项目可以按需有偿讲解,提供后续答疑。

运行效果
运行 main.m
图 1: 各信号波形
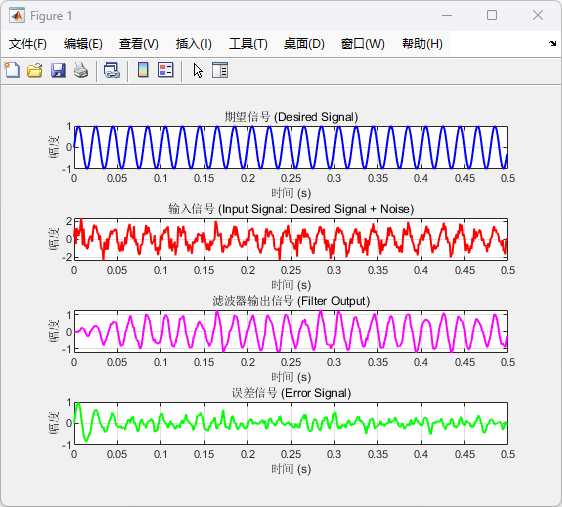
第一行 (期望信号):
(1)这是理想的正弦波信号(50 Hz)。
(2)不含噪声,表示目标信号。
第二行 (输入信号):
(1)由期望信号加上高斯白噪声组成。
(2)显示带噪环境下的信号波形。
第三行 (滤波器输出信号):
(1)经LMS滤波器处理后的输出信号。
(2)显示噪声抑制后的信号,较接近期望信号。
第四行 (误差信号):
(1)表示期望信号与滤波器输出信号之间的误差。
(2)误差的大小反映了滤波器的性能。
图 2: 滤波器权重变化
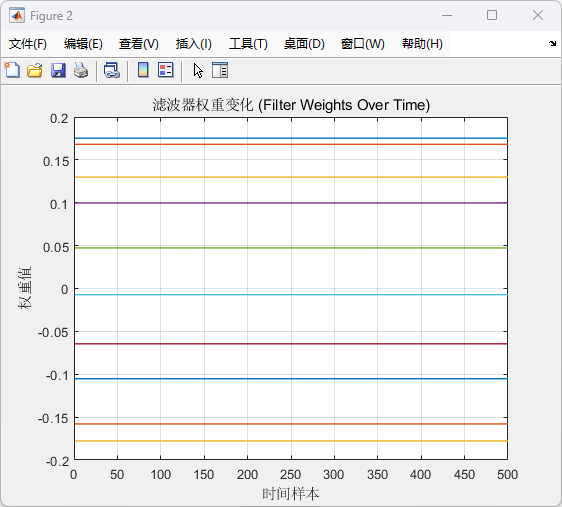
(1)显示LMS滤波器在整个迭代过程中权重的变化。
(2)权重最终收敛到某些稳定值,反映滤波器适应输入信号的能力。
(3)权重曲线说明滤波器如何调整自身以最小化误差信号。
图 3: 不同步长因子下的误差信号
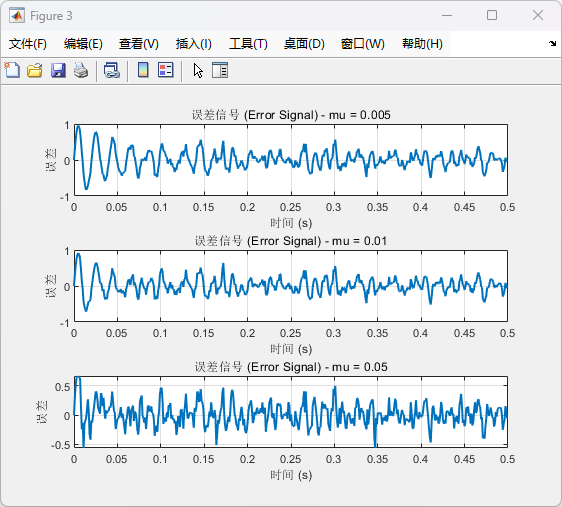
mu = 0.005:
(1)步长较小,权重更新较慢,收敛时间较长。
(2)误差下降平缓,噪声抑制效果略慢。
mu = 0.01:
(1)中等步长,平衡了收敛速度和稳定性。
(2)收敛较快,误差下降较为平稳。
mu = 0.05:
(1)步长较大,权重更新速度快。
(2)初期误差下降迅速,但可能引入不稳定性或振荡。
图 4: 命令行文本输出信息
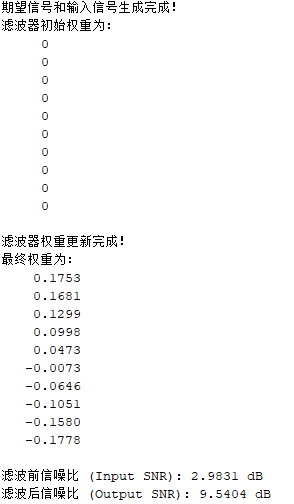
1.滤波器初始权重:权重初始化为零,开始时滤波器不具备任何先验知识。
2.滤波器更新权重:显示最终权重值,反映了滤波器对信号特性的学习结果。
3.信噪比 (SNR):
(1)滤波前 SNR (2.9831 dB):输入信号中噪声较多,信噪比较低。
(1)滤波后 SNR (9.5404 dB):经滤波后,信噪比显著提升,滤波器有效地降低了噪声干扰
总结:通过上述分析,LMS滤波器能够从带噪信号中提取期望信号,并显著提高信噪比。步长因子对收敛速度和稳定性影响显著,应根据实际需求进行合理选择。
远程部署
Tipps:购买后可免费协助安装,确保运行成功。
– 远程工具:Todesk 、向日葵远程控制软件
– 操作系统:Windows OS
项目文件

文件目录
Tipps:完整项目文件清单如下:
项目目录
– 1.Code (完整代码:确保运行成功)
– 2.Result (运行结果:真实运行截图)
– 3.Demo (演示视频:真实运行录制)



评论(0)