随着现代信号处理技术的快速发展,噪声消除技术在许多领域中占据了重要地位,如语音信号处理、无线通信系统、图像处理以及工业控制系统。在实际应用中,噪声的存在会显著降低信号的质量和系统的性能,如何高效地消除噪声成为研究的热点。本文围绕基于 LMS(Least Mean Squares,最小均方)自适应滤波算法的噪声消除技术展开研究,并构建了一个完整的噪声消除系统。通过 MATLAB 平台实现该算法,并针对不同的滤波器阶数(Filter Order)和学习率(Nu)参数,全面评估了算法的性能,包括误差性能、收敛特性以及信噪比(SNR)的提升效果。
项目信息
编号:MOG-76
大小:10M
运行条件
Matlab开发环境版本:
– Matlab R2020b、2023b、2024a
项目介绍
随着现代信号处理技术的快速发展,噪声消除技术在许多领域中占据了重要地位,如语音信号处理、无线通信系统、图像处理以及工业控制系统。在实际应用中,噪声的存在会显著降低信号的质量和系统的性能,如何高效地消除噪声成为研究的热点。本文围绕基于 LMS(Least Mean Squares,最小均方)自适应滤波算法的噪声消除技术展开研究,并构建了一个完整的噪声消除系统。通过 MATLAB 平台实现该算法,并针对不同的滤波器阶数(Filter Order)和学习率(Nu)参数,全面评估了算法的性能,包括误差性能、收敛特性以及信噪比(SNR)的提升效果。
实验结果表明,LMS 自适应滤波算法在不同的参数设置下表现出较强的鲁棒性和适应性,能够有效降低目标信号中的噪声,显著提高信号的信噪比(SNR)。进一步分析表明,滤波器阶数与学习率对算法的收敛速度和稳态误差具有显著影响:较大的滤波器阶数能够提升滤波器的建模能力,但可能导致收敛速度的降低;较高的学习率可以加快收敛速度,但可能引入更大的稳态误差。此外,本文通过对学习曲线和残差信号的深入分析,揭示了算法的动态特性和滤波效果,展示了 LMS 算法在不同应用场景中的适应能力。
本文的研究不仅验证了 LMS 自适应滤波算法在噪声消除中的高效性和稳定性,还为优化算法参数提供了指导建议,为未来进一步改进噪声消除技术和开发相关应用提供了理论基础和实践参考。未来的研究可在此基础上结合其他自适应滤波算法(如 NLMS 和 RLS),进一步提升噪声消除系统的性能,以满足更复杂场景中的需求。
项目文档
Tipps:可以根据您的需求进行写作,确保文档原创!
– 项目文档:写作流程

算法流程
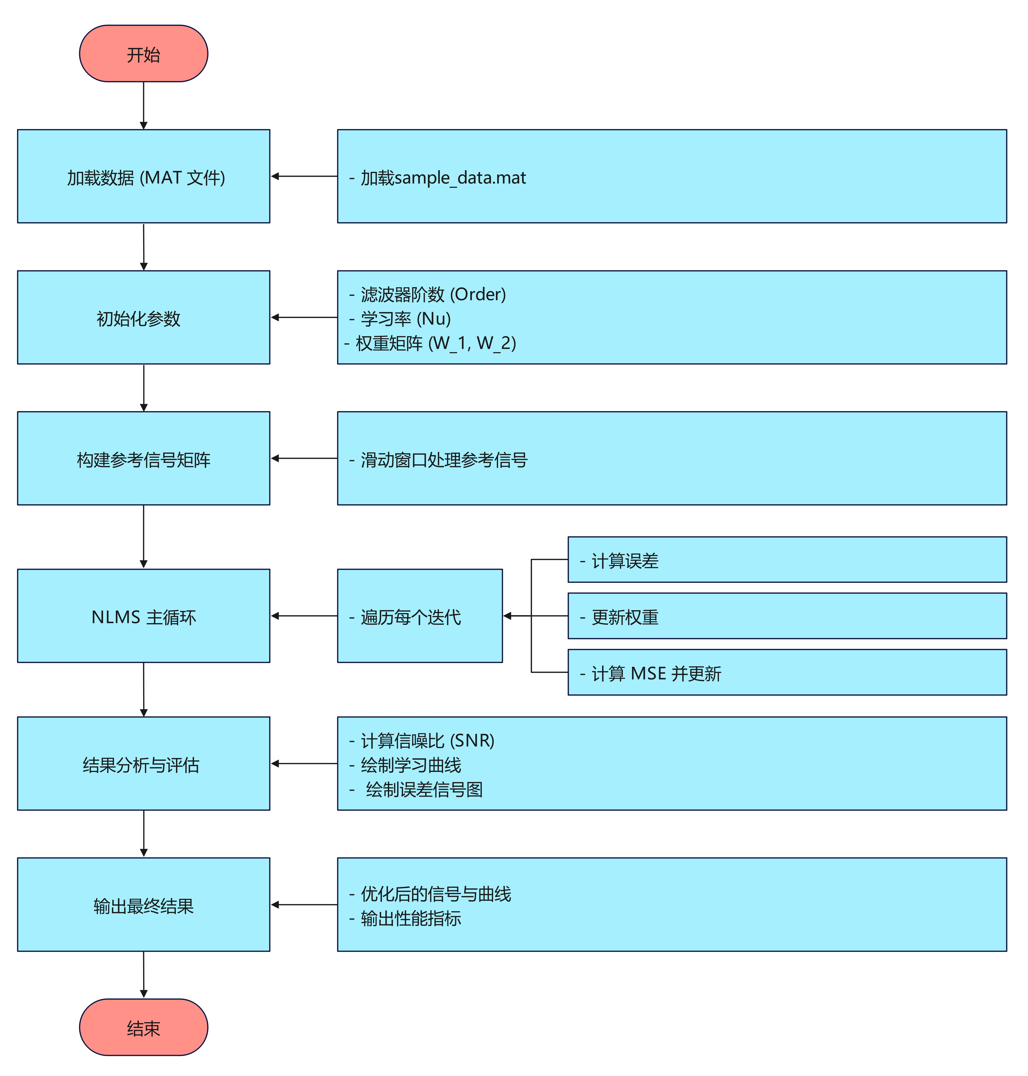
代码讲解
Tipps:仅对运行AdaptiveFilterAlgorithm.m部分代码简要讲解。该项目可以按需有偿讲解,提供后续答疑。

运行效果
运行 AdaptiveFilterAlgorithm.m
图1:Learning Curve For Filter Order = 50 and Iteration < 46.5K
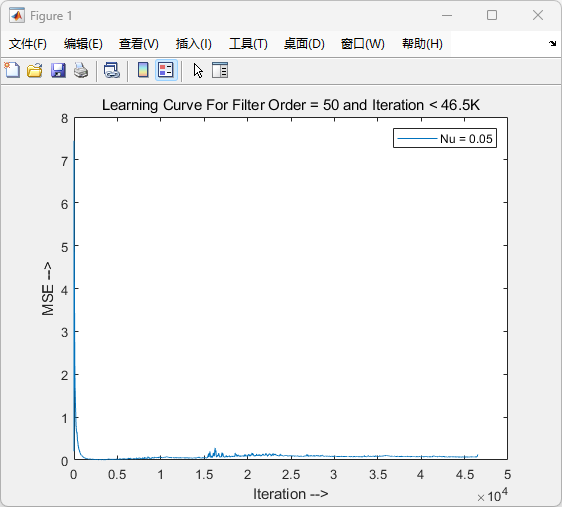
含义:
(1)这是滤波器在迭代次数小于 46,500 时的学习曲线,表示误差(MSE,Mean Squared Error)随迭代次数的变化。
观察:
(1)初始误差较大,随着迭代次数的增加,误差迅速下降并趋于稳定。
(3)说明滤波器在早期阶段快速学习并适应了输入信号。
图2:Learning Curve For Filter Order = 50 and Iteration > 46.5K
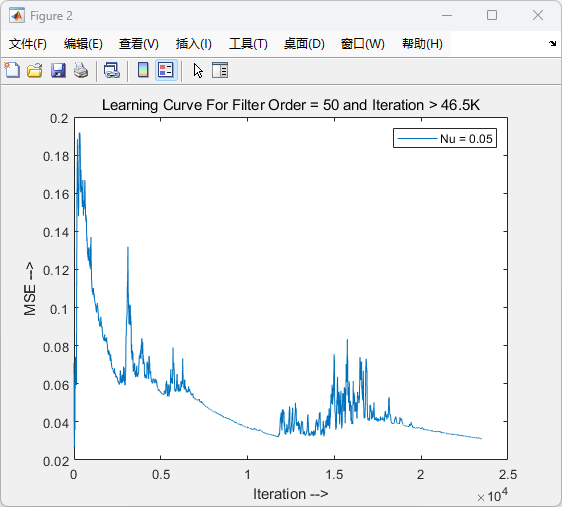
含义:
(1)这是滤波器在迭代次数大于 46,500 时的学习曲线,表示误差随迭代次数的变化。
观察:
(1)误差(MSE)在较大的迭代次数范围内逐渐下降,但比前一阶段收敛速度慢,且存在一些波动。
(2)说明滤波器在后期更难以显著改进,但仍有一定优化。
图3:Error Signal After Applying NLMS For Filter Order = 50
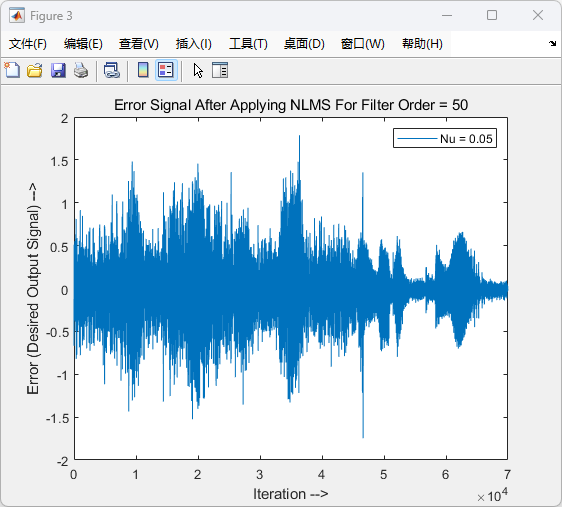
含义:
(1)显示应用 NLMS 滤波器后,滤波器输出信号与期望信号之间的误差(残差信号)随迭代次数的变化。
观察:
(1)初始误差较大,随着迭代次数增加,误差信号逐渐减小。
(2)图中后期误差的波动幅度减小,说明滤波器已经有效抑制了大部分噪声,剩余误差主要是小幅波动。
总结:
(1)图1和图2分别展示了不同阶段的学习过程,说明滤波器可以有效减少信号误差。
(2)图3展示了滤波器的最终性能,表明 NLMS 算法能够较好地抑制噪声,但误差信号中仍存在部分难以完全消除的高频波动。
远程部署
Tipps:购买后可免费协助安装,确保运行成功。
– 远程工具:Todesk 、向日葵远程控制软件
– 操作系统:Windows OS
项目文件
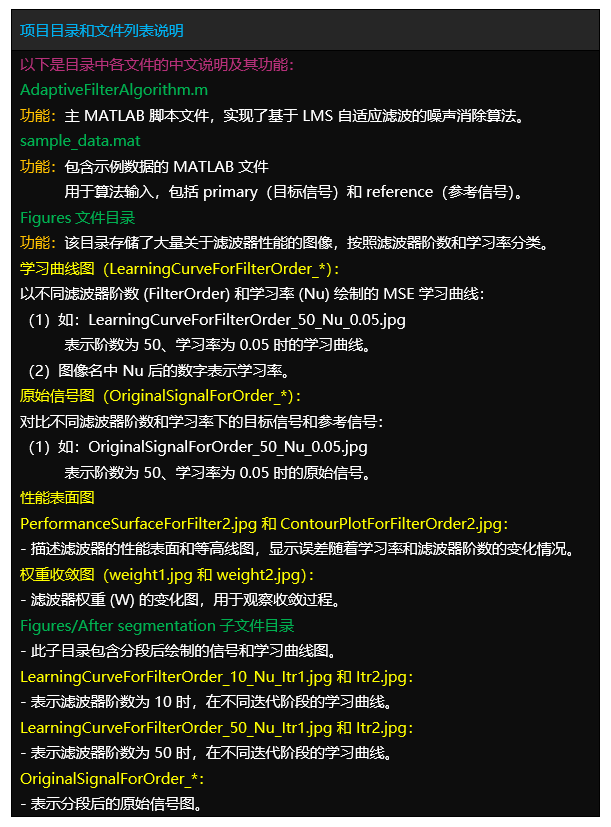
文件目录
Tipps:完整项目文件清单如下:
项目目录
– 1.Code (完整代码:确保运行成功)
– 2.Result (运行结果:真实运行截图)
– 3.Demo (演示视频:真实运行录制)



评论(0)