变分模态分解(Variational Mode Decomposition, VMD)是一种现代信号处理方法,能够将复杂信号分解为若干具有特定频率特性的模态分量,为信号的特征提取与分析提供了有力工具。本文首先介绍了VMD的基本理论与算法框架,并对其核心参数(带宽约束参数、模态数、收敛精度等)进行了详细讨论。随后,通过将低频、中频、高频分量及噪声构建复合信号,验证了VMD算法在频域分解与时域重建方面的有效性。实验结果表明,VMD能够准确提取信号的本征模态函数,各模态的频率与输入信号分量的频率高度吻合。本文的研究为VMD在工程信号处理、故障诊断、生物医学信号分析等领域的应用奠定了理论基础。
项目信息
编号:MOG-73
大小:2M
运行条件
Matlab开发环境版本:
– Matlab R2020b、2023b、2024a
项目介绍
变分模态分解(Variational Mode Decomposition, VMD)是一种现代信号处理领域中的新兴方法,它通过优化信号分量的变分模型,能够将复杂信号分解为若干具有特定频率特性的模态分量(Intrinsic Mode Functions, IMFs),从而实现信号的精细化分解与多尺度特征提取。相比于传统的信号分解方法,如经验模态分解(Empirical Mode Decomposition, EMD)和小波变换(Wavelet Transform),VMD以其严格的数学基础、鲁棒的分解性能以及对噪声干扰的高容忍性在信号分析中显示出显著优势。本文系统地介绍了VMD的基本理论与算法框架,包括其对带宽约束的描述、模态中心频率的自适应优化以及收敛精度的控制机制。同时,针对VMD算法中关键参数(如带宽约束参数、模态数目、收敛阈值等)的设置对分解效果的影响进行了深入探讨。
为了验证VMD算法的有效性,本文构建了一个包含低频、中频、高频分量以及随机噪声的复合信号,利用VMD对该信号进行分解,并分别从频域和时域对分解结果进行分析。实验结果表明,VMD能够准确提取信号的本征模态函数,各模态的频率特征与输入信号分量的频率高度吻合。同时,分解后模式的频谱分布清晰且相互独立,体现了良好的频带分离能力。此外,分解出的时域信号重建结果与原始信号高度一致,验证了VMD在时域信号重构方面的有效性和可靠性。
本文的研究表明,VMD是一种高效且精准的信号分解工具,可广泛应用于工程信号处理、机械故障诊断、生物医学信号分析、地震波分析等多个领域,为复杂信号的多尺度分解和特征提取提供了坚实的理论支持和技术保障。同时,本文的研究为VMD在更广泛领域的应用探索提供了重要参考,并为后续研究的参数优化和算法改进奠定了基础。
项目文档
Tipps:可以根据您的需求进行写作,确保文档原创!
– 项目文档:写作流程

算法流程
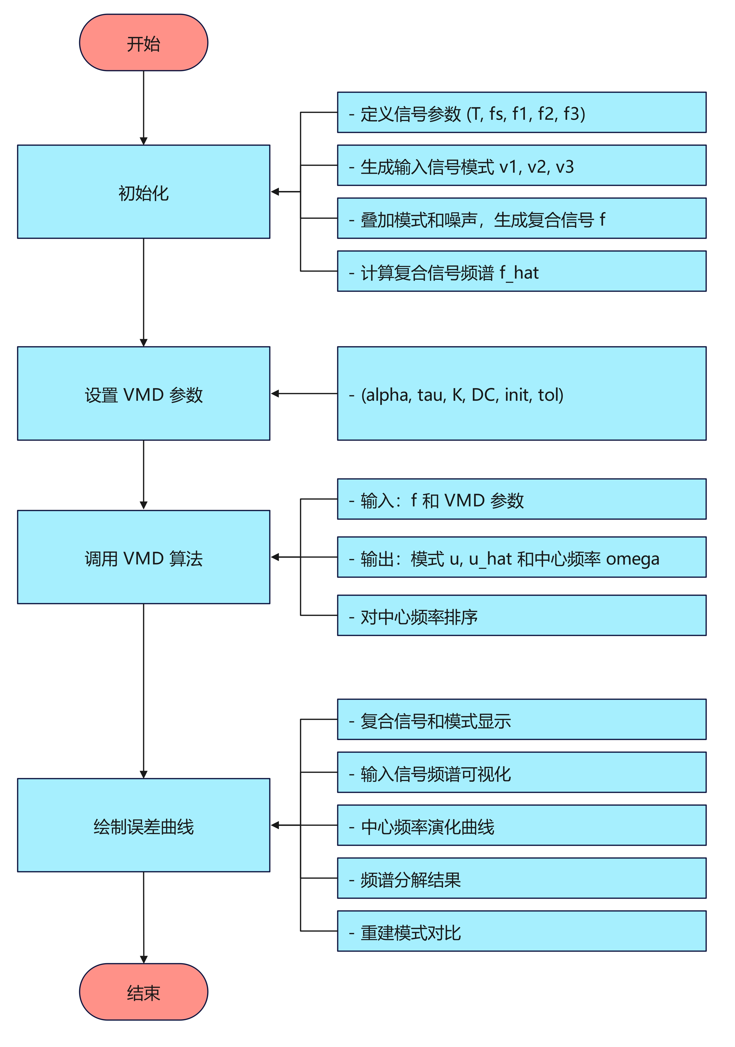
代码讲解
Tipps:仅对运行LSTM_mian.m部分代码简要讲解。该项目可以按需有偿讲解,提供后续答疑。

运行效果
运行 LSTM_mian.m
图 1:Composite input signal(复合输入信号)
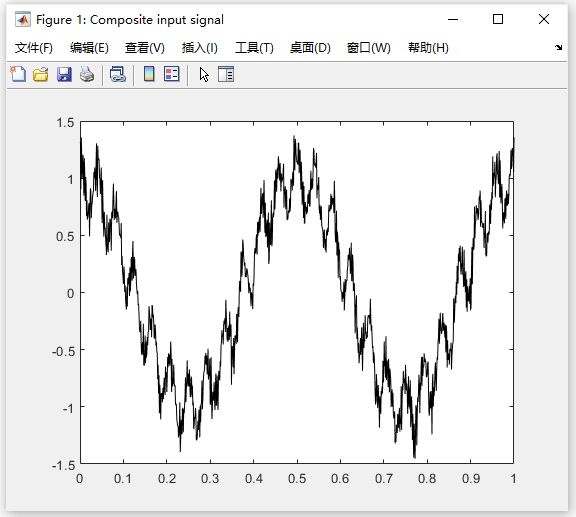
图 2:Input signal component 1(输入信号分量 1)
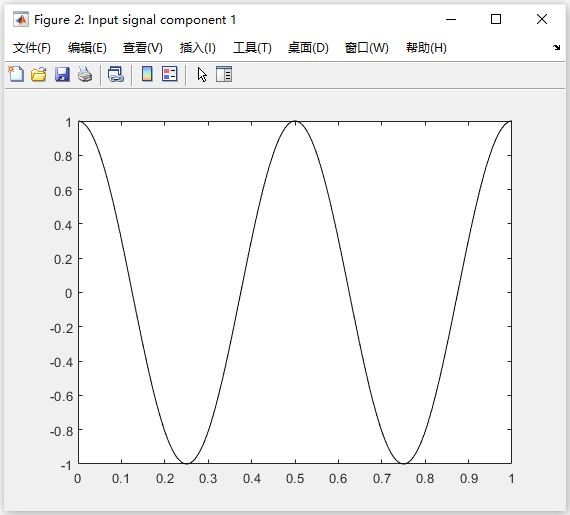
图 3:Input signal component 2(输入信号分量 2)
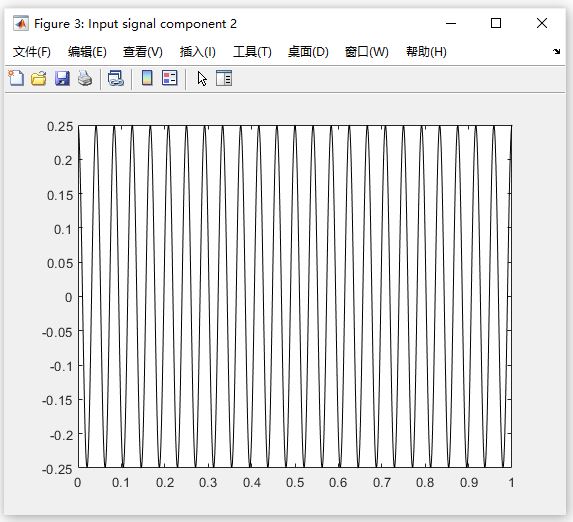
图 4:Input signal component 3(输入信号分量 3)
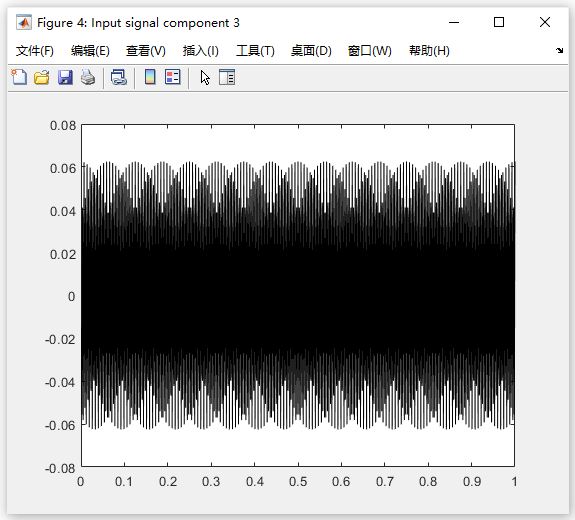
图 5:Input signal spectrum(输入信号的频谱)
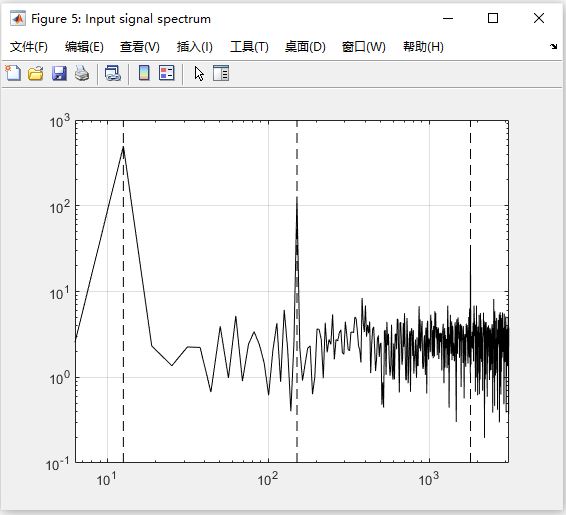
图 6:Evolution of center frequencies omega(中心频率的演化过程)
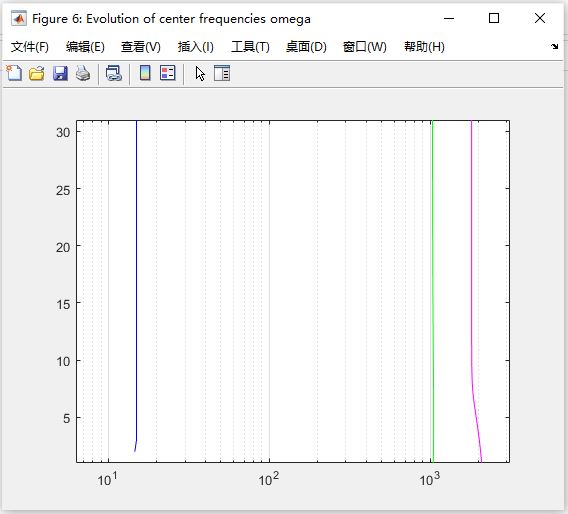
图 7:Spectral decomposition(频谱分解)
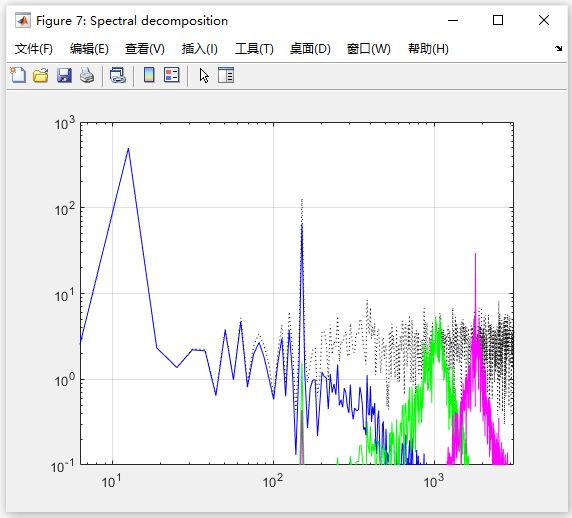
图 8 对应最低频模式(Mode 1)
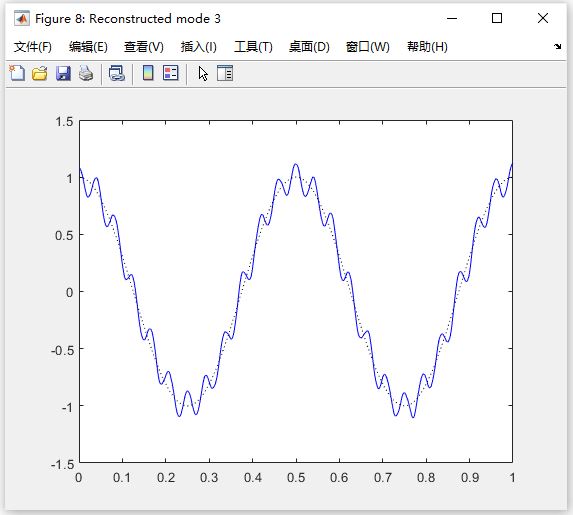
图 9 对应中频模式(Mode 2)
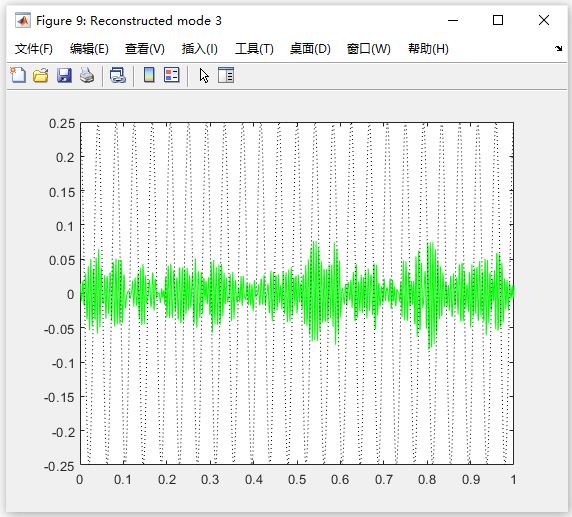
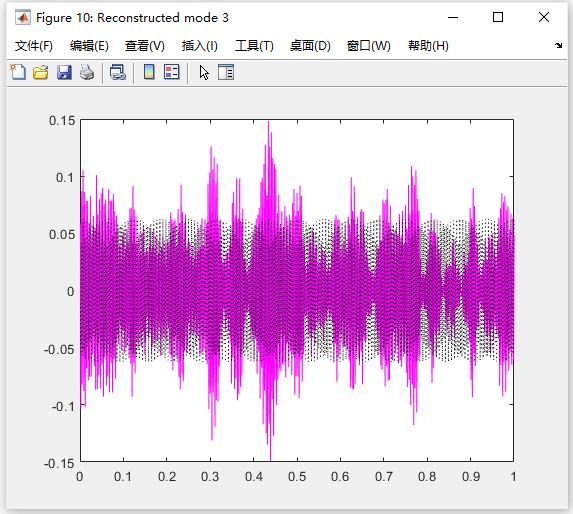
图 10 对应高频模式(Mode 3)
远程部署
Tipps:购买后可免费协助安装,确保运行成功。
– 远程工具:Todesk 、向日葵远程控制软件
– 操作系统:Windows OS
项目文件
文件目录
Tipps:完整项目文件清单如下:
项目目录
– 1.Code (完整代码:确保运行成功)
– 2.Result (运行结果:真实运行截图)
– 3.Demo (演示视频:真实运行录制)



评论(0)