本研究并实现了一种基于Matlab的蚁群算法,用于解决路径规划问题。
项目信息
编号:MOG-49
大小:4.3M
运行条件
Matlab开发环境版本:
– Matlab R2021b
项目介绍
本文研究并实现了一种基于Matlab的蚁群算法,用于解决路径规划问题。传统蚁群算法在复杂环境中的路径规划时,容易陷入局部最优解,导致收敛速度较慢。为此,本文提出了一种改进的蚁群算法,结合了撤回机制,增强了算法的路径搜索能力和全局优化能力。通过与传统蚁群算法和不含撤回机制的算法进行对比,实验结果表明,改进算法在收敛速度和路径规划效果方面具有显著优势。本文的研究为进一步优化蚁群算法在实际路径规划中的应用提供了理论依据和技术支持。
项目文档
Tipps:可以根据您的需求进行写作,确保文档原创!
– 项目文档:写作流程

算法流程
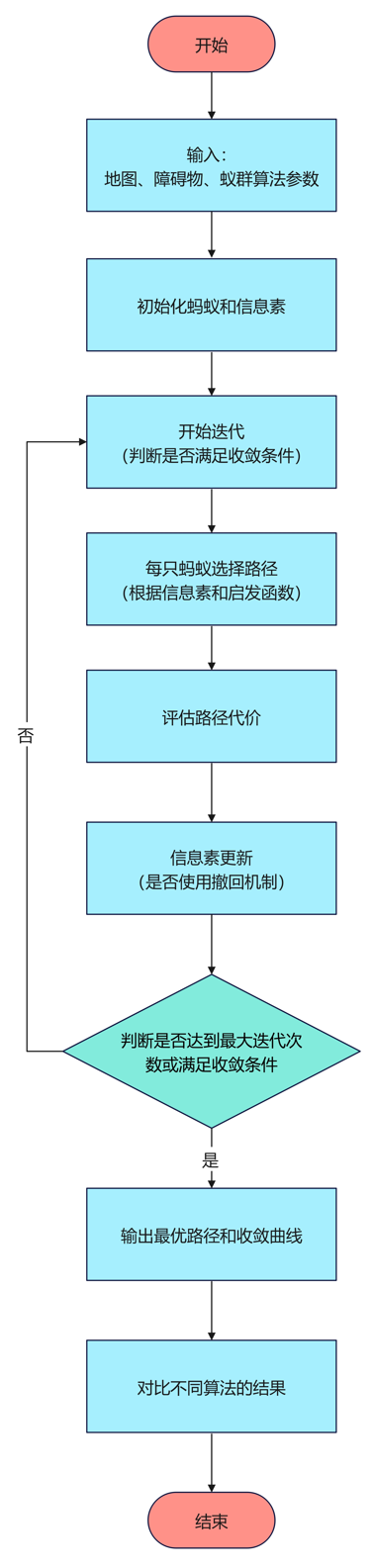
代码讲解
Tipps:仅对improved_ant.m部分代码简要讲解。该项目可以按需有偿讲解,提供后续答疑。
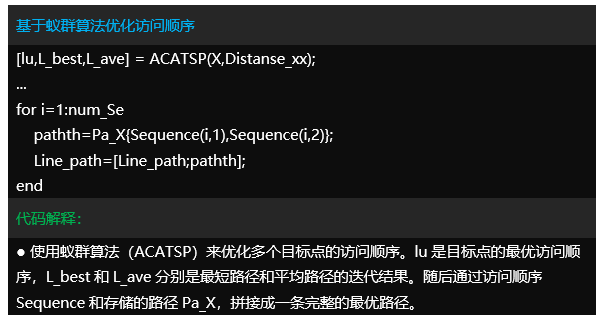
运行效果
运行 improved_ant.m
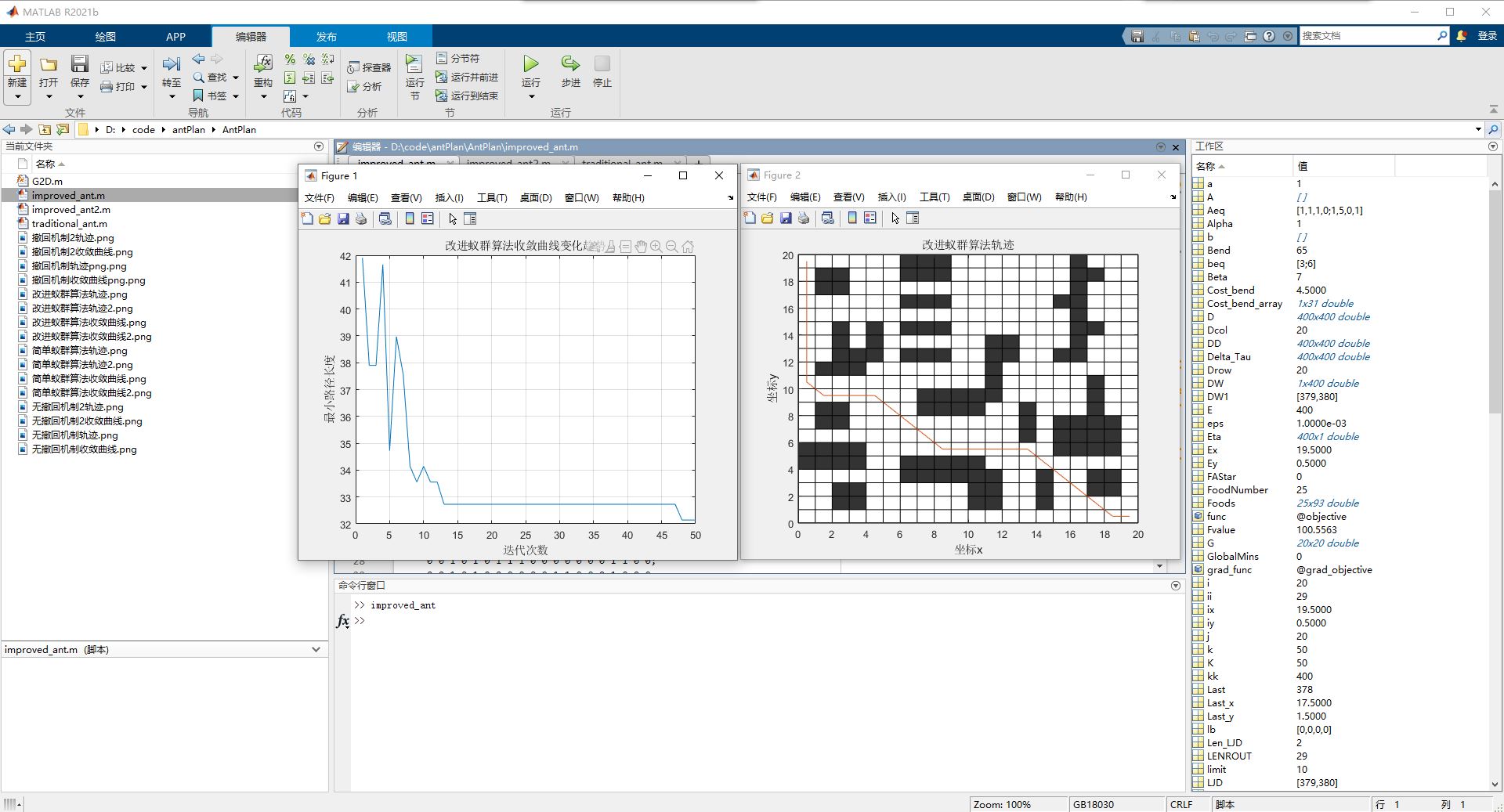
(1)左侧的图展示了收敛曲线,显示了随着迭代次数(选择代次数)的增加,**路径代价(适应度)**如何下降。该曲线表明算法收敛速度较快,在大约10次迭代后稳定下来。早期的急剧下降表明优化效果较好。
(2)右侧的图展示了路径规划图(改进蚁群算法轨迹)。这个网格图可能代表环境,黑色的方块表示障碍物。橙色的线条表示算法找到的轨迹,显示算法成功地绕开障碍物规划了路径。
运行 improved_ant2.m
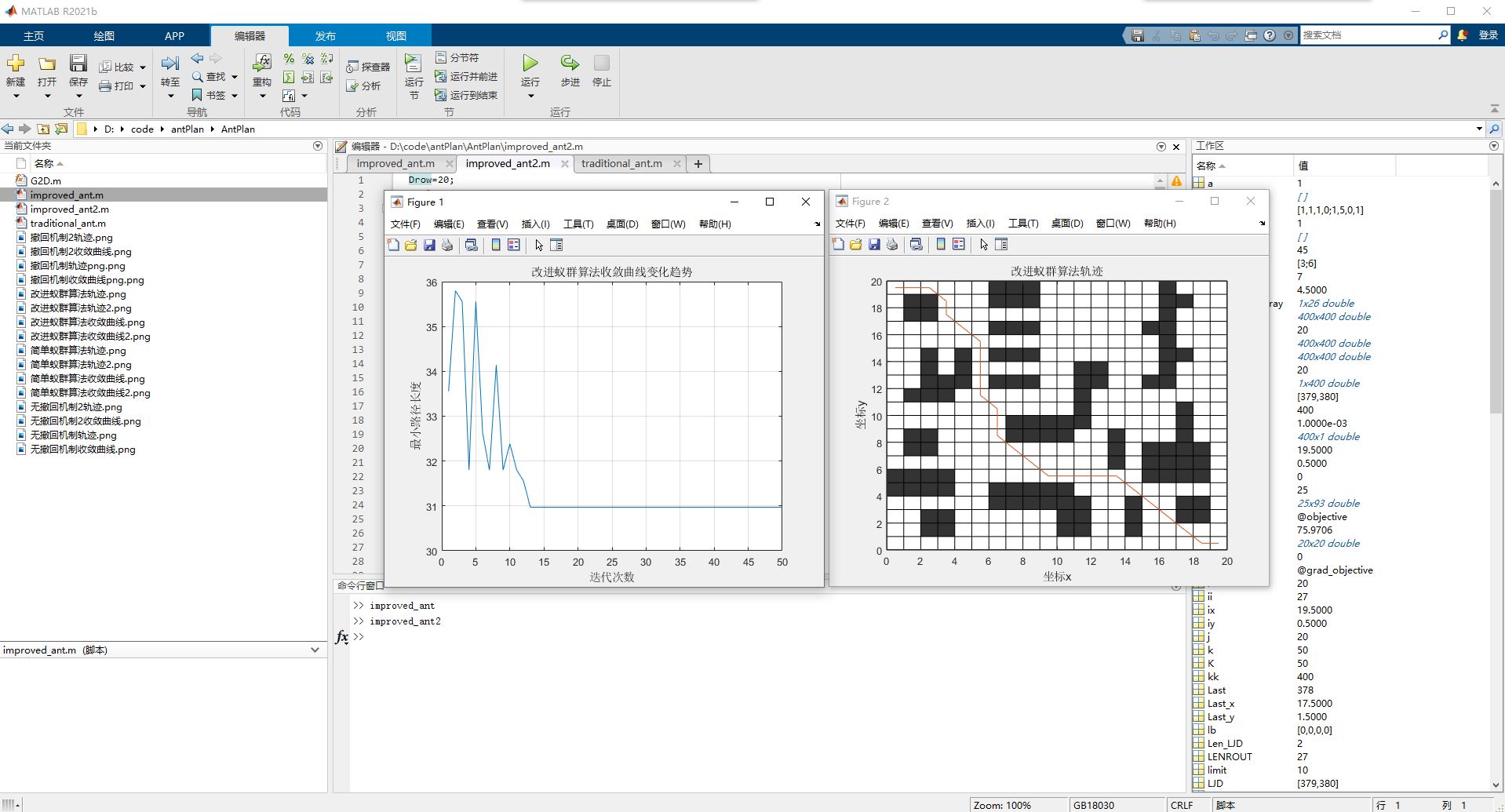
(1)左侧的图同样是收敛曲线,但这是第二种改进算法的表现(改进蚁群算法收敛曲线变化趋势)。初始路径代价值大约为36,经过轻微波动后,约在第10次迭代后稳定下来。
(2)右侧的图与第一张图类似,是路径规划图,显示了第二种改进算法的路径。该路径成功避开了障碍物,顺利到达目标。
运行 traditional_ant.m
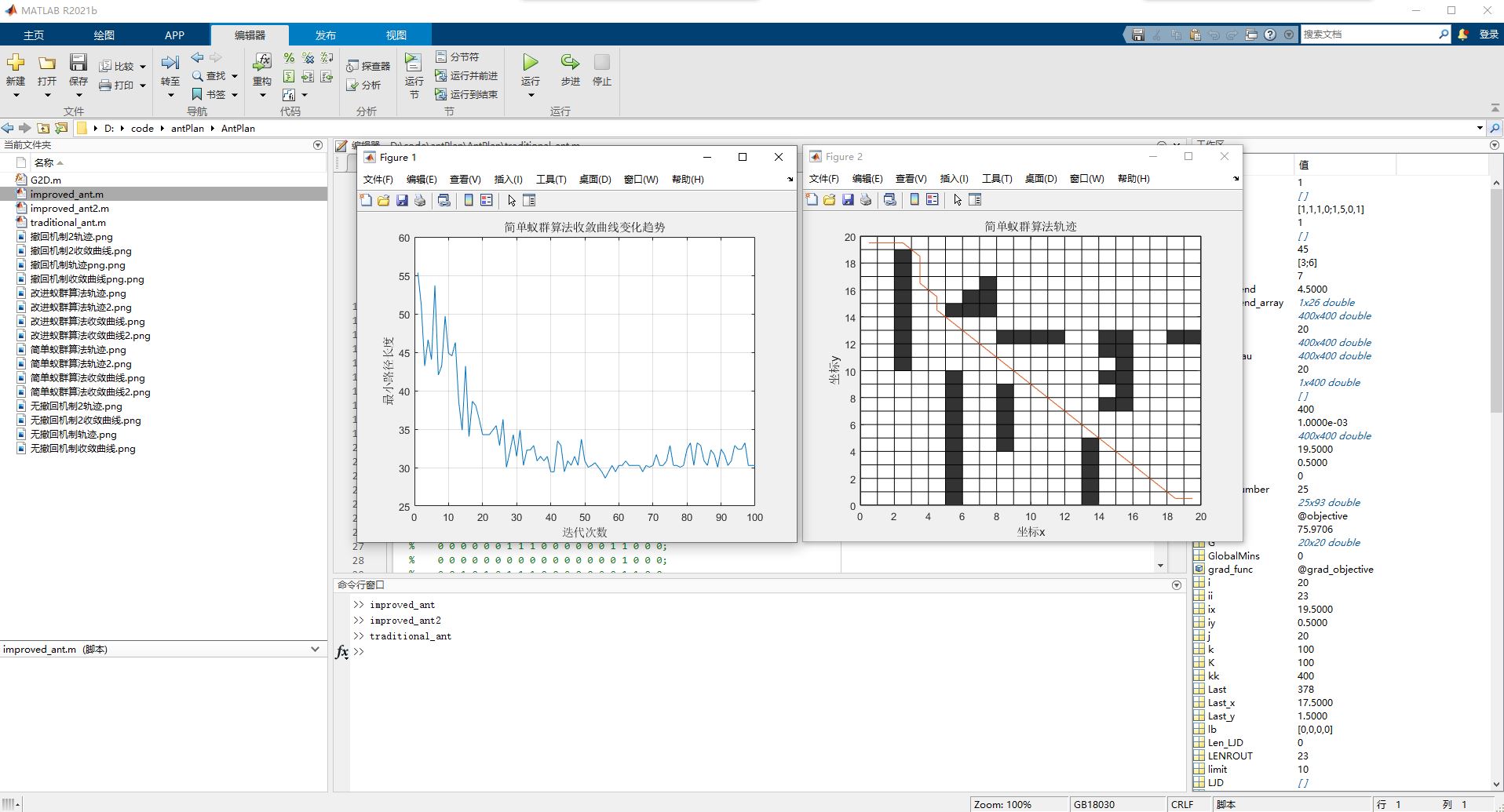
(1)左侧的图展示了传统蚁群算法(简单蚁群算法)的收敛曲线。与改进的算法相比,这条曲线更为不规则,收敛速度较慢,稳定前需要更多的迭代次数。这表明该算法在找到最优路径时效率较低。
(2)右侧的图是传统算法的轨迹图,与前面类似。此算法的路径看起来更加曲折,可能反映了其路径规划优化较差。
这几张图比较了两种改进的蚁群优化算法与一种传统蚁群算法,并显示了改进算法在收敛速度和路径优化上的显著提升。
远程部署
Tipps:购买后可免费协助安装,确保运行成功。
– 远程工具:Todesk 、向日葵远程控制软件
– 操作系统:Windows OS
项目文件

文件目录
Tipps:完整项目文件清单如下:
项目目录
– 1.Code (完整代码:确保运行成功)
– 2.Result (运行结果:真实运行截图)
– 3.Demo (演示视频:真实运行录制)



评论(0)